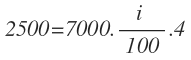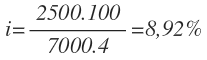Propiedades de Existencia del Triángulo

PROPIEDADES DE EXISTENCIA DEL TRIANGULO

 El propósito de esta experiencia es que los estudiantes aprendan a construir triángulos haciendo uso de la regla y el compás. También, expresar con dibujos, construcciones con regla y compás, con material concreto, y con lenguaje geométrico, su comprensión sobre la “propiedad de la existencia de un triángulo”. 

Reto: Construir un triángulo rectángulo considerando que uno de sus lados es un segmento de longitud 10 cm. También, escribir el procedimiento que realizaste y dar 3 ejemplos de situaciones prácticas en los que se podrían usar los triángulos rectángulos.

¿Cuál crees que sea el polígono más simple?

Los triángulos se utilizan con frecuencia en el diseño de estructuras, ya que brindan rigidez y equilibrio en la construcción, tal es el caso en las torres de alta tensión, puentes, estanterías removibles, entre otros. Conocer las características y propiedades de los triángulos te ayudará a comprender su importancia en el diseño y construcción.

Responde las siguientes preguntas:

a.     ¿Qué es un polígono?En geometría, un polígono es una figura geométrica plana compuesta por una secuencia finita de segmentos rectos consecutivos que encierran una región en el plano.​ Estos segmentos son llamados lados, y los puntos en que se intersecan se llaman vértices.

b.     ¿Qué es un triángulo?Se llama triángulo o trígono, en geometría plana, al polígono de tres lados. Los puntos comunes a cada par de lados se denominan vértices del triángulo.​Un triángulo tiene tres ángulos interiores, tres pares congruentes de ángulos exteriores, ​ tres lados y tres vértices entre otros elementos.

¿Conoces las propiedades de un triángulo?

Ahora te invito a resolver las siguientes situaciones considerando los siguientes procesos

Ø  Lee bien el problema hasta comprenderlo

Ø  Busca una estrategia y aplícala

Ø  Reflexiona sobre tus resultados obtenidos

Elvis va a ayudar a su hermano a cercar un corral con alambre para que sus animales no se escapen. Para ello han colocado estacas en tres de sus esquinas y, luego, han marcado con cal la línea por donde pasará el alambre. Así han obtenido un triángulo, al medir sus ángulos, noto que estaban en relación de 3 a 4 y que el suplemento del tercer ángulo era 98°

Te invito a resolver las siguientes preguntas:

·         ¿Qué ángulos forman los lados del corral?

·         ¿Qué propiedad aplicarías?

Para consolidar tus aprendizajes te invito a resolver la siguiente situación, no olvides comprobar los resultados obtenidos

Ø  A José le encargaron elaborar un espejo en forma triangular cuyas medidas de sus ángulos sean proporcionales a 5, 6 y 7

¿Cuánto miden los ángulos interiores que deberá tomar en cuenta José?

Para reafirmar tus conocimientos  te invito a visitar  y leer este documento:
Conociendo los triángulos

RETO
El propósito de esta experiencia es que los estudiantes aprendan a construir triángulos haciendo uso de la regla y el compás. También, expresar con dibujos, construcciones con regla y compás, con material concreto, y con lenguaje geométrico, su comprensión sobre la “propiedad de la existencia de un triángulo”. Reto: Construir un triángulo rectángulo considerando que uno de sus lados es un segmento de longitud 10 cm. También, escribir el procedimiento que realizaste y dar 3 ejemplos de situaciones prácticas en los que se podrían usar los triángulos rectángulos.

Realiza un organizador visual con los datos que consideres más importantes .

Las magnitudes

LAS MAGNITUDES

¿Por qué es necesario seleccionar y usar unidades y subunidades para estimar y medir magnitudes derivadas como la velocidad?

Iniciaremos respondiendo las siguientes interrogantes:

a.     ¿Qué son las magnitudes? ¿Que podemos medir?

b.     ¿Cómo podemos expresar la velocidad en relación a la distancia y al tiempo? ¿Cuál es la unidad de longitud? ¿ En que se mide el tiempo? Propón algunos ejemplos

c.     ¿Como podemos expresar la velocidad , si esta es constante, en función de la distancia y el tiempo? La unidad de la velocidad es……m/s

d.     Si un automóvil viaja en línea recta y se controla su recorrido en 3 puntos. En un primer momento el automóvil avanza 30m/s; en el segundo.150m en 5s;y en el tercero avanza 240m en 8s, completa la tabla

En un primer momento el automóvil avanza 30m/s	V=  30m/1s
en el segundo.150m en 5s	V=  150m/5s   V=  30m/1s
en el tercero avanza 240m en 8s	V=  240m/8s   V=  30m/1s

Como aprecias la velocidad las 3 velocidades son iguales, se determina por la división de la distancia entre el tiempo transcurrido entonces     v=d/t

Ahora te invito a resolver las siguientes situaciones considerando los siguientes procesos

Ø  Lee bien el problema hasta comprenderlo

Ø  Busca una estrategia y aplícala

Ø  Reflexiona sobre tus resultados obtenidos

SITUACIÓN PROPUESTA.

El presidente Martín Vizcarra, ha transferido 300 millones para 1874 municipios, entre distritales y provinciales, con la finalidad de repartir productos de primera necesidad a las familias más vulnerables en este periodo de emergencia. Dos municipalidades de la región Junín (nos reservaremos los nombres) se unieron y contrataron un camión para trasladar los productos a sus localidades, el camión llevo los víveres a la municipalidad A, donde descargó y entregó al responsable del almacén los productos para luego dirigirse al municipio B. Al revisar los productos y cotejando con la pecosa se dieron cuenta en la municipalidad A, que habían recibido 100kg de arroz y 2 cajas de leche más de lo que les correspondía, el encargado muy preocupado por los productos que faltarían en la municipalidad B y eso afectarían a familias necesitadas, tomo la camioneta de la municipalidad y fue al alcance del camión para entregarle lo que no le correspondía. En ese instante el camión había avanzado 3000m en línea recta y viajaba con una velocidad de 30m/s y para alcanzarlo la camioneta corrió a una velocidad de 180km/h.

Según la información recibida, responde las siguientes interrogantes:

a.     ¿Con la velocidad que corre la camioneta alcanza o no al camión? Justifica tu respuesta

Sabemos que la camioneta es de  180km/h.=180000m/3600s= 50m/s concluyendo que como es mayor que 30m/s la camioneta si alcanza al camión.

b.     ¿En cuánto tiempo la camioneta alcanza al camión? ¿Qué distancia tendrá que recorrer la camioneta para dar alcance al camión? Si el camión baja a 30m/s y la camioneta lo sigue a 50m/s y las velocidades son constantes podemos afirmar que la camioneta se acerca a una velocidad de 20m/s(50-30), ahora dividimos 3000m /20m/s tiempo en que lo alcanza será de 150s que transformando a minutos tendremos 150s/60s = 2minutos y 30 segundos

c.     Que distancia tendrá que recorrer la camioneta para alcanzar al camión? 150s entonces v=d/t y d= vt entonces tenemos d= 50m/s. 150s =   7500m por lo que afirmamos que la camioneta avanza 7500m para alcanzar al camión,

d.     ¿En qué tipo de familias se formarán las personas responsables y honestas? Si todos actuaríamos de manera solidaria y responsable ¿cómo crees que avanzaríamos como país? Reflexiona las respuestas con tu familia

Para ello analizaremos una situación

Si un automóvil viaja en línea recta, cuyo recorrido se controla en tres puntos:

·         En el primer punto el automóvil avanza 30m en 1 segundo

·         En el segundo punto el automóvil avanza 150m e 5 segundos

·         En el tercer punto el automóvil avanza 240m en 8 segundos

¿Cómo determinamos la velocidad en los tres puntos?

RETO

Para consolidar tus aprendizajes te invito a resolver la siguiente situación, no olvides comprobar los resultados obtenidos

Ø En la comunidad de Anta en la región Cusco, dos amigos Ricardo y Martin se retan una carrera de bicicletas, dando una ventaja de 100m a Ricardo porque su bicicleta es un poco más pequeña que la de Martin, se sabe que Ricardo maneja a una velocidad de 8m/s y Martín corre a una velocidad de 36km/h, ¿En qué tiempo alcanza Martin a Ricardo? ¿Cuál es la distancia que recorre Martin para alcanzar a Ricardo y Cuál es la distancia recorrida por Ricardo antes de ser alcanzado

Rpta. Martín corre a una velocidad de 36km/h= 36000m/3600s= 10m/s

Si sabemos que Ricardo maneja a una velocidad de 8m/s y Martín  a10m/s entonces Distancia que recorre Martin para alcanzar a Ricardo y las velocidades son constantes podemos afirmar que la Martin se acerca a Ricardo a una velocidad de 2m/s  ( 10-8m/s) ahora dividimos 100m /2m/s tiempo en que lo alcanza será de 50s .

INTERES SIMPLE

¿Qué es el interés del dinero?

¿QUE ES INTERES?

El interés es el beneficio que genera una determinada cantidad de dinero, como por ejemplo en un préstamo o en un depósito a plazo fijo. Es proporcional a la cantidad de dinero prestada y al tiempo que dura el préstamo o el plazo fijo.

Es decir, si una entidad financiera presta dinero a alguien, esa persona, deberá devolver la cantidad prestada más el interés, que es el beneficio de la entidad financiera por prestar ese dinero.

De la misma forma, si depositas un plazo fijo en un banco, el banco te ofrece un beneficio al final de un periodo de tiempo, por lo que recibirás el dinero depositado más el interés, que será el beneficio obtenido por realizar un plazo fijo.

Existen dos tipos de intereses: interés simple e interés compuesto. El interés simple es algo más sencillo de calcular, pero el compuesto requiere de una fórmula más complicada. Si quieres calcularlo de forma sencilla, aquí tienes una calculadora del interés compuesto, que te será de gran utilidad.

No hay que confundir los intereses, que es una cantidad de dinero determinada, con el tipo o la tasa de interés, que es un porcentaje y que te explico en el siguiente apartado.

Conceptos relacionados con el interés

Vamos a explicar los conceptos que necesitas conocer para entender bien el interés, ya que necesitas tenerlo muy claros para identificarlos y saber trabajar con ellos en los ejercicios sobre interés, que veremos más adelante:

Capital

Tenemos dos tipos de capitales:

• El capital inicial, que es la cantidad de dinero inicial que se presta o se deposita.
• El capital final, que es la cantidad de dinero obtenida después de sumarle los intereses

Tasa o tipo de interés

Es el porcentaje en el que se van generando los intereses en cada periodo que dura el préstamo o el depósito. Está muy relacionado con el periodo de tiempo que dura el préstamo, ya que el tipo de interés puede ser anual, semestral, trimestral, mensual…

Se puede expresar en tanto por uno o en tanto por ciento, teniendo en cuenta que al expresarlo en tanto por uno, hay que dividirlo entre 100:

Y si lo expresamos en tanto por ciento, ya está dividido entre 100 directamente:

Al final, el valor es el mismo:

En los ejercicios sobre interés simple e interés compuesto se suele trabajar siempre en tanto por uno, ya que es la forma de expresarlo más comúnmente.

Periodo de tiempo

Es el tiempo durante el cual el capital prestado o depositado está generando intereses. Puede medirse en años, semestres, trimestres, meses…

Interés simple

¿Cómo se calcula el interés simple?

El interés simple se calcula siempre sobre el capital inicial. Los intereses generados en cada periodo de tiempo es siempre el mismo.

Por ejemplo, en el caso de prestar o depositar 1000 € al 5% anual. ¿Cuántos intereses se generarían en un año?

Sólo hay que calcular el 5% de 1000 € y tendríamos los intereses generados, multiplicando el capital inicial por el porcentaje en tanto por ciento o en tanto por uno y dividiéndolo entre 100.

Lo calcularemos con el tipo de interés en tanto por uno:

Por tanto, en un año se generarían 50 €.

¿Cuántos intereses se generarían en 8 años?

Pues sólo tenemos que multiplicar la cantidad anterior por el número de años que dura el préstamo o el depósito, ya que cada año se generan los mismos intereses:

Para calcular el capital final, sumamos los intereses a al capital inicial:

Por tanto, para calcular el interés simple, podemos utilizar la siguiente fórmula:

Donde, «Ci» es el capital inicial prestado o depositado, «i» es el tipo de interés (en tanto por uno, porque lo dividimos entre 100) y «t» es el tiempo que dura el préstamo o el depósito.

El tipo o tasa de interés y el periodo de tiempo, deben expresarse en la misma unidad de tiempo. Es decir, si el tipo de interés es anual, el periodo de tiempo debe estar en años, si el tipo de interés es mensual, el tiempo debe estar en meses y así sucesivamente.

Lo más fácil es pasar siempre el periodo de tiempo a la unidad en la que esté expresada el tipo de interés.INTERES SIMPLE

Ejercicios resueltos sobre interés simple

Vamos a resolver algunos ejercicios sobre interés simple para que te quede más claro todo lo que acabo de explicar:

Ejercicio 1

¿Cuál es el interés simple generado en un plazo fijo, por un capital de 10000 €, al 4% trimestral durante 2 años?

Aplicamos la fórmula del interés simple:

Pero tenemos en cuenta que el tipo de interés está en trimestres y el periodo de tiempo en años. Por tanto, debemos pasar los años a trimestres, multiplicando por 4, ya que un año tiene 4 trimestres:

Ejercicio 2

Hace 4 años de pidió un préstamo de 7000 € y la cantidad pagada al terminar el periodo del préstamo han sido 9500 €. ¿Qué tipo de interés se le aplicó?

En este caso el capital inicial son 7000 €, pero cuidado, porque los intereses generados no son 9500 €. Los 9500 € corresponden al capital final.

Por tanto, calculamos los intereses generados en primer lugar:

Ahora sustituimos todos los datos en la fórmula del interés simple:

Y despejamos el tipo de interés:

Es un tipo de interés anual, ya que el periodo de tiempo estaba en años.

FUNCIONES LINEALES

¿QUE ES UNA FUNCION?

Es una correspondencia entre los elementos de un conjunto de partida llamado dominio y los elementos de un conjunto de llegada llamado codominio de tal forma que los elementos se corresponden uno a uno.

...y¿que es una funcion lineal?

1. Una función lineal es una función cuyo dominio son todos los números reales, cuyo codominio son también todos los números reales,y cuya expresión analítica es un polinomio de primer grado. 
2.              F(x): R —> R  /  f (x) = ax + b  ,donde a y b son números reales, es una función lineal. se lee:   f de R en R tal que f de equis es igual a  ax + b 

1. Ejemplos: 
2. Algunas representaciones de funciones lineales: 
3. y = x 
4. f (x) = x + 2 
5. h (x) = (x + 5) 
6. g (x) = ¼ x - ¼ 
7. y = 5x - ½ 
8. Características de la función lineal: 
9. 1) Se representa por y = m · x ± b 
10. 2) m representa un número ℝ y se le llama pendiente. b es un valor constante y pertenece al conjunto ℝ . 
11. 3)Si m tiene signo positivo, la función lineal crece. 
12.    Si m tiene signo negativo, la función lineal decrece. 
13.   4)El punto (0, b), es el punto donde la función corta el eje de las ordenadas (y). 
    
14. 
    
15. 
    
16.  Representar la función y = x Tabulando la función:  Cuando no se establece que conjunto numérico tomara el dominio y codominio se deduce que será los ℝ. La función y = x; nos dice que el valor que tome la variable “x” debe ser igual al valor de variable “y”. Observa el siguiente video 
17. https://www.youtube.com/watch?v=AoZpzAoC1Qg

Otra grafica de una funcion es:

RETO

REALIZA LA TABLA DE VALORES DE LA FUNCIÓN  F(X)= 2X+3 Y REALIZA SU GRAFICA, INDICA LOS PARES ORDENADOS Y SEÑALA EL DOMINIO Y CODOMINIO DE LA FUNCION DADA